Nel libro “Curve Policentriche” appare chiaro come il luogo di equidistanza tra due cerchi di raggio differente sia una conica e, pertanto, come diventi facile tracciare tangenti ad essi quanti cerchi si vogliano.
Con il presente studio mi sono proposto di verificare cosa succeda nel caso in cui si applichino sulla superficie sferica le stesse regole.
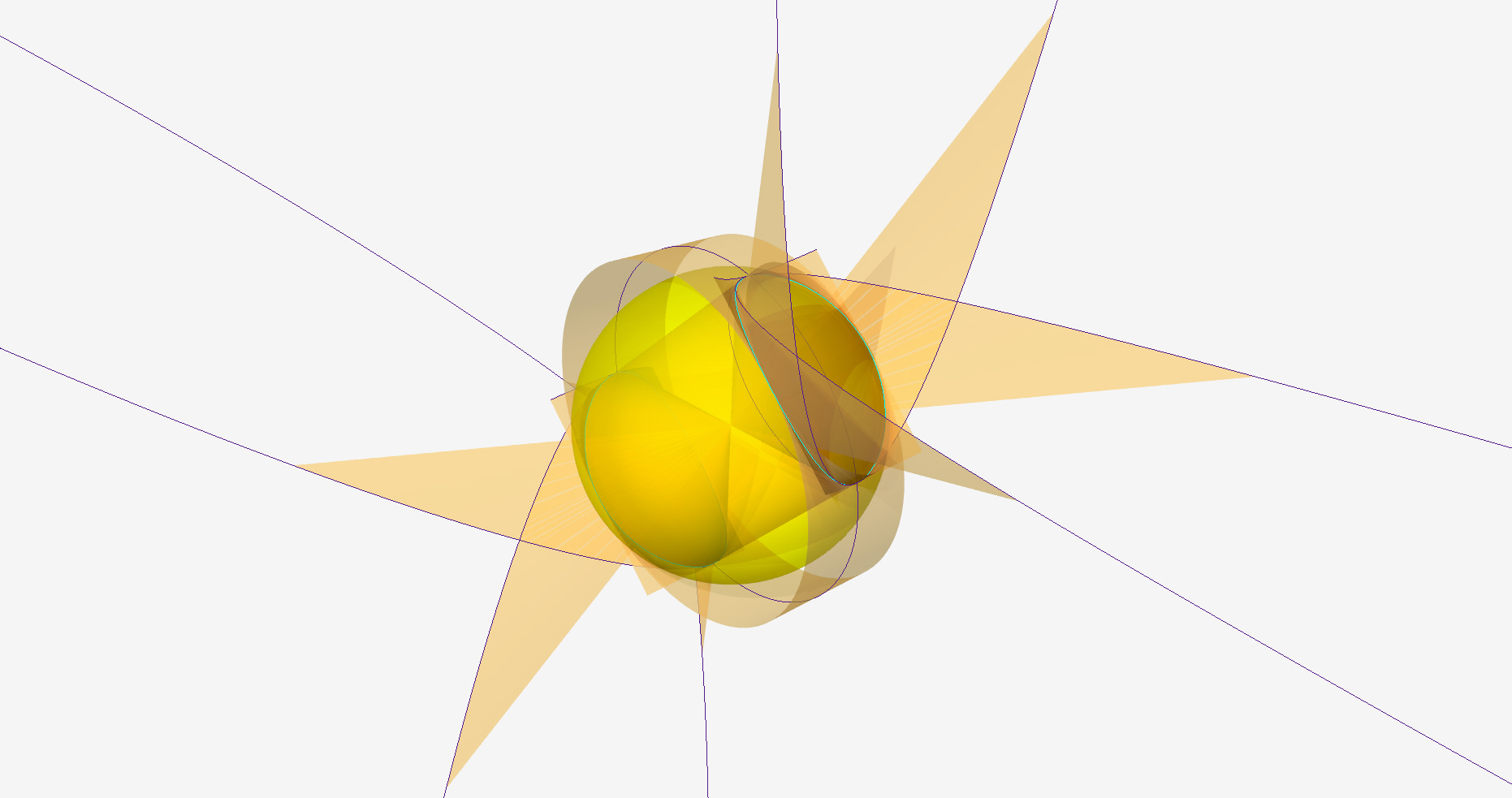
Mi sono subito accorto di un un fatto che non può non sorprendere, dato che si allontana dal senso comune. Il fatto è che le coniche da tre sono diventate una. La linea che sulla superficie sferica possiede le caratteristiche di luogo di equidistanza tra due cerchi dati ha, al tempo stesso, le proprietà che nel piano distintamente hanno Ellisse, Iperbole e Parabola. Per questo motivo ho chiamato tale curva PaIpEll, un nome che accorpa le iniziali delle tre parole.
Lo studio si compone di una parte a carattere generale e di una serie di esemplificazioni basate sulle differenti modalità di rapportarsi tra i cerchi.
Al momento le esemplificazioni mostrate sono soltanto due su diciotto in preparazione.
Per apprezzare gli effetti delle Stop Motion si consiglia di scaricare il file.
Spherical conics
Mutazioni delle coniche su sfera Pdf
PaIpEll-testo Pdf

LdE A su sfera Cerchio Max Cerchio asecante

LdE B su sfera Cerchio Max Cerchio asecante
